What is a Random Variable?
The term "Random Variable" is used extremely often within the realm of probability and statistics, but what does it mean? Well, a random variable is defined as a variable whose possible values are outcomes of a random phenomenon. In specific terms, it is a function that maps the outcomes of an unpredictable process in numerical terms, often represented as a real number. So, a random variable may represent the outcome of an experiment that has yet to be performed, or a value that is currently uncertain. However, there are a couple of properties that are required of random variables.
A random variable conveys the results of an objectively random process, like rolling a die, or a subjectively random process, like an individual who is uncertain of an outcome due to incomplete information. A random variable must be measurable, which allows for the assignment of probabilities to the potential outcome. Furthermore, its outcome sometimes depends on environmental factors, like wind during a coin toss, however these additional factors are often excluded.
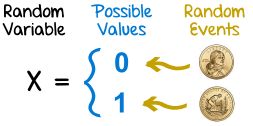
Image credit: http://www.mathisfun.com
Random variables have a domain defined by the set of all possible outcomes of an event. Additionally, they have a probability distribution. This distribution can be either continuous, measuring numerical values in an interval, or discrete, as specified by a list of countable values. Within probability theory, random variables are used as functions defined by a sample space whose outcomes are numerical values.
Applications of Random Variables
As mentioned above, random variables are very common within almost any facet of mathematics and/or the scientific method and are often used in computer science. Random variables can be either discrete or continuous, as defined by the context of their application.
Discrete - Coin Toss
Imagine a coin toss where, depending on the side of the coin landing face up, a bet of a dollar has been placed. The possibility of winning a dollar corresponding to the outcome of a coin toss before tossing the coin defines the random variable. The outcome of the coin toss is either heads, or tails, creating an equal probability of either outcome. Because the value of the random variable is defined as a real-valued dollar, the probability distribution is discrete.
Continuous - Height
Any random variable that is defined through measuring, rather than counting, is continuous. In this case, imagine wanting to study the effects of caffeine intake on height. One's height would be the continuous random variable as it is unknown before the completion of the experiment, and its value is taken from measuring within a range.
Random Variables in Machine Learning
Random variables are an invaluable tool within applications of machine learning. As a neural network makes decisions using machine learning, it creates functions for understanding possible outcomes. These possible outcomes are often defined by random variables.
